自転車のタイヤが軽くなると漕ぎ出しも軽くなるのか?
(自転車の運動エネルギーとタイヤの回転エネルギーを比べてみた)
2020/09/29: 発行
目次
1. はじめに
以前こちらの記事におきまして、太いタイヤと細いタイヤでは、相応の理由があって細いタイヤの方が漕ぎ出しが軽くなるとお伝えしました。

自転車のタイヤは細いほど漕ぎ出しが軽い
その後別の読者の方より、タイヤが軽くても漕ぎ出しが軽く感じるとので、これについても弊サイトで取り上げてほしいとのメールを頂きました。
本件につきましては、タイヤが地面に接触している限り、車両の総重量が同じであればタイヤが重くなろうが軽くなろうが車両の加速には関係しないとお伝え(詳細はこちら)ているのですが、体感では違いを感じられるとの事です。
特に自転車のタイヤは径が大きいので、クルマのタイヤうり重さによる影響が出易いのではないかとも考えられている様です。
こうなると実際に実験をしてみるしかないと思いながらも、もしかしたら自転車の運動エネルギーとタイヤの回転エネルギーを計算したら何か分かるかもしれないと思い、試しに計算してみる事にしました。
そんな訳で、どんな結末になるか全く分からないまま書き進めていきますので、余り大きな期待はせずにお読み頂けると助かります。
2. 自転車の運動エネルギー
それでは先ず、自転車の運動エネルギーを求めてみたいと思います。
例えば、重さ60kgの人が重さ20kgの自転車に乗って、直線路を時速30kmで走っているとします。

時速30kmで走る総重量80kgの自転車の運動エネルギーはいくらか
この場合の自転車の運動エネルギーは、いくらになるでしょうか。
物体の運動エネルギーはご存知の通り1/2mv² (mが質量で、vが速度)で求められますので、この自転車の運動エネルギーは以下の様になります。
| 自転車の運動エネルギー | =1/2mv² |
| =1/2×80kg×(30km/h)² | |
| =1/2×80kg×(30km×1000m/km÷h×3600s/h)² | |
| =1/2×80kg×(30000m÷3600s)² | |
| =40kg×69.4m²/s² | |
| =2777kg・m²/s² | |
| =2777J |
答えはご覧の通り2777Jになります。
2777Jと聞いてもピントこないと思いますが、これは100Wの電球を27.8秒間点灯させられるだけのエネルギーになります。
そう聞くと、電気のありがたさを痛感します。
それはともかく、この運動エネルギーに更にタイヤが回転している事による回転エネルギーを追加する方はいらっしゃらないでしょう。
もしそうだとしたら、タイヤが重くなろうが軽くなろうが、自転車の総重量が同じならば漕ぎ出しの力は同じ筈です。
とは言いても、いや正確にはタイヤの回転エネルギーも入れるべきだと言われそうなので、次に行きます。
3. タイヤの回転エネルギー
本書としては、(くどい様ですが)あくまでもタイヤの回転エネルギーは自転車が直線に進む運動エネルギーに含まれると考えているのですが、折角ですので勉強がてらにタイヤの回転エネルギーを求めてみようではありませんか。
もしかしたら何か分かるかもしれません。
回転する物体の運動エネルギーは、(直線運動する物体の運動エネルギーに似て)1/2Iω² で求められます。
ここで”I(アイ)”とは慣性モーメントの事で、”ω(オメガ)”は角速度を表わします。
それでは分かり易い様に、”I(アイ)”と”ω(オメガ)”を個別に計算して、最後に回転エネルギーを求めてみます。
慣性モーメント
先ず慣性モーメント(I)とは、下の図の様に回転する物体が動き続け様とする量を表し、重さに比例し、尚且つ回転中心から物体までの距離の2乗に比例します。
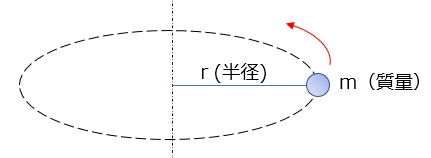
慣性モーメント(I)は、重さに比例し、回転中心から物体までの距離の2乗に比例する
自転車のタイヤは中空のドーナツ形状ですが、ここでは手っ取り早く下の様な平らなリング形状だとして、慣性モーメントを計算してみます。
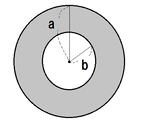
この場合の慣性モーメントは以下の式で求められます。
| 慣性モーメント | =1/2(a²+b²)×m |
ここで、スポーツ自転車のタイヤの外形(直径)を0.7mとするとaが0.35m、25Cのタイヤの太さを25mmとするとbは0.325m(=0.35m-0.025m)になり、25Cのタイヤの重さは0.4kg(400g)になります。
これを先ほどの式に当てはめますと、タイヤの慣性モーメントは以下の様になります。
| 慣性モーメント | =1/2((0.35m)²+(0.325m)²)×0.4kg |
| =1/2×(0.12m²+0.11m²)×0.4kg | |
| =0.046m²・kg |
角速度
次に角速度(ω)は、単位時間当たりの回転角をラジアンで表示したものです。
仮に自転車が時速30kmで走行しているとしたら、タイヤの外形が0.7mですので、以下の様にタイヤは1秒間に3.8回転している事になります。
| 時速30kmでのタイヤの回転数 | =(30km×1000m/km)÷2×π×0.35m |
| =30000m÷2.2m | |
| =13636回転/時間 | |
| =3.8回転/秒 |
これをラジアン単位の角速度(ω)で表示すると、3.8回転/秒に2π(2パイ)ラジアンを掛けて7.6π(7.6パイ)ラジアン/秒になります。
| 角速度 | =3.8回転/秒×2πラジアン |
| =7.6πラジアン/秒 | |
| =23.9ラジアン/秒 |
更に、ご存知の様にπ(パイ)は3.14ですので、7.6πラジアン/秒は最終的に23.9ラジアン/秒になります。
回転エネルギー
この慣性モーメントと角速度を、先ほどの式1/2Iω² に入れると、タイヤの回転エネルギーは以下の様になります。
| 回転エネルギー | =1/2Iω² |
| =1/2×(0.046m²・kg)×(23.9/秒)² | |
| =13kg・m²/s² | |
| =13J |
いかがでしょう?
自転車のタイヤは2本あるので、タイヤの回転エネルギーが2倍の26Jとしても、自転車の運動エネルギーである2777Jと比べると、こんなにも小さい(1%未満)のです。
にも関わらず、これで漕ぎ出しの力に差が生じるものでしょうか?
4. タイヤが重くなった場合の回転エネルギー
そうは言っても、まだご納得頂けないでしょうから、次にこのタイヤがもっと重くなった場合に、回転エネルギーがどれくらい増えるかも見てみます。
今まではタイヤの重さは0.4kgでしたが、思い切って2倍の0.8kgにしてみます。
この場合、ママチャリのタイヤである35Cと同じくらいの重さになります。
さてここで事前に予想して頂きたいのですが、これによってタイヤの回転エネルギーはどれくらい増えると思われるでしょうか?
2倍でしょうか、5倍でしょうか、はたまた10倍でしょうか?
自転車の場合タイヤの径が大きいので、タイヤの重さが2倍になると、その回転エネルギーは一気に数倍に跳ね上がる様な気がしませんでしょうか?
そんな期待を胸に、先ず重さが2倍になったタイヤの慣性モーメントを求めると、以下の様になります。
| 慣性モーメント | =1/2(a²+b²)×m |
| =1/2((0.35m)²+(0.325m)²)×0.8kg | |
| =1/2×(0.12m²+0.11m²)×0.8kg | |
| =0.092m²・kg |
角速度は前回と同じですので、これで回転エネルギーを求めてみます。
| (回転エネルギー) | =1/2Iω² |
| =1/2×(0.092m²・kg)×(23.9/秒)² | |
| =13kg・m²/s² | |
| =26J |
ご覧の様に2倍の26Jになりました。
何もわざわざ計算しないでも2倍になるのは分かっていたのですが、敢て計算してみました。
ご覧の様に自転車の様に径の大きなタイヤであっても、タイヤの重さが2倍になっても回転エネルギーは2倍にしかならないのです。
自転車の運動エネルギーである2777Jに対して、タイヤ2本でも52Jです。
これでもうある程度ご納得頂けるのではないでしょう。
前段でお伝えしました様に、仮に自転車の運動エネルギーとは別にタイヤの回転エネルギーが存在しているとしても、その値は自転車の運動エネルギーと比べれば無視できるほど小さいのです。
さらにタイヤの重さが2倍になった所で、タイヤの回転エネルギーは2倍になるものの、やはり自転車の運動エネルギーと比べれば微々たるものなのです、
にも関わらず、タイヤが多少重くなった程度で、漕ぎ出しの重さが変わったと気付くものでしょうか?
気付かないとみるのが妥当ではないでしょうか?
5. 実験
そうは言ってもまだご納得頂けない方もいらっしゃる事でしょう。
そうなれば、実際にタイヤを重くしてタイヤだけの漕ぎ出しの力を体感して頂くしかありません。
この実験は非常に簡単です。
先ず自転車をスタンドに立てかけて、後輪を浮かせます。
その状態でペダルを手で回します。
次にタイヤを重くします。
もし100g重くしたいのであれば、10円玉1個が4.5gですので、10円玉を23個均等にタイヤに貼り付けます。
それで再度ペダルを手で回して、その重さを前回と比べます。
果たして差を感じる事ができるものでしょうか?
多少のプラセボ効果でもしかしたら重くなったと感じるかもしれませんが、ならば足でペダルを踏んで、その差を感じる事ができるでしょうか?
恐らくどなたも感じる事はできないのではないでしょうか。
ましてや同じサイズの自転車用のタイヤでしたら、下の表にあります様に重さの差は数十gしかありません。
| タイヤの太さ | 空気圧 | 質量 | 用途 |
|---|---|---|---|
| 23C | 105PSI | 380g | ロードバイク |
| 25C | 100PSI | 400g | ロードバイク |
| 28C | 95PSI | 440g | クロスバイク |
| 32C | 80PSI | 540g | クロスバイク |
| 35C | 75PSI | 790g | ママチャリサイズ |
| 37C | 70PSI | 1020g | ワイド系 |
ですので、同じサイズのタイヤが重くなっても、タイヤを空転させた場合のペダルを漕ぐ力の差など誰にも分かる筈はありません。
にも関わらずタイヤを普通に接地させた状態で自転車を漕いで、タイヤの重さの差を感じる事ができるでしょうか?
どう考えても、無理だと思うのですが、いかがでしょうか?
6. まとめ
それではまとめです。
①もし走行中の自転車の運動エネルギーとタイヤの回転エネルギーが別々に存在するとしても、前者に対して後者は無視できるほど小さい。
②またタイヤの重さが2倍になっても、タイヤの回転エネルギーは2倍になるだけで、やはり自転車の運動エネルギーと比べれば微々たるものである。
③さらに後輪のタイヤを浮かした状態で、タイヤの重さを多少変えた所で、ペダルを踏む力の差など誰にも分からない。
④以上の事から、もし自転車の運動エネルギーとタイヤの回転エネルギーが別々に存在するとしても、タイヤが重くなって漕ぎ出しの力が変わるとは思えない。
なお弊サイトとしましては、あくまでも漕ぎ出しに関する重さは自転車の総重量であり、タイヤの重さは関係しないと固く信じています事付け加えておきます。
自転車のタイヤが軽くなると漕ぎ出しも軽くなるのか?
(自転車の運動エネルギーとタイヤの回転エネルギーを比べてみた)
(自転車の運動エネルギーとタイヤの回転エネルギーを比べてみた)