タイヤを太くしてもグリップは変わらない
(常識を覆すタイヤの太さとグリップの関係)
2017/05: 発行
目次
1. はじめに
タイヤは太いほどグリップ良いのか?
本書では過去よりタイヤは太くなってもグリップは変わらないと主張しているのですが、依然そうではないとする意見も根強く残っているのも事実です。
実際その様に主張するサイトも多数存在しますし、本サイトにも同様のメールを何度か頂く事があります。
このため、従来の記事を全面改訂して、実例を上げながらこの件を掘り下げていこうと思います。
恐らくこれを読んでもご納得頂けない方も多いとは思いますが、多少面白い話も盛り込んでおきましたので、騙されたと思って読んで頂ければ幸甚です。
2. 接地面積と摩擦力の関係
恐らくこれをお読みになる大多数の方は、タイヤは太い程グリップは良くなると思われている事でしょう。
実際レーシングカーはやたらに太いタイヤを履いています。

太いタイヤを履いたレーシングカー
どころが全くそんな事はないのです。
すなわち、タイヤを太くしてもグリップは変わらないのです。
そんな訳はないと思われる方に、質問です。
以下の図の様に、倉庫の作業員が段ボールの箱を床を滑らせながら運んでいました。
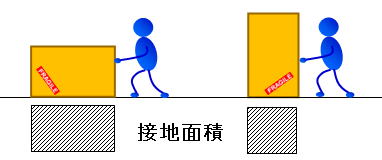
この場合、箱を寝かせた場合と立てて滑らせた場合で、どちらが楽に(軽く)動かせるでしょうか?
何となく接地面積が小さい方が押す力も小さくて済む様な気がしますが、どちらも押す力は同じなのです。
もし手元に消しゴムがあったら、机の上で立てた場合と寝かせた場合でどちらが重いか鉛筆で押してみれば、感覚的に分かって頂けると思います。
これが何を意味するかと言えば、段ボール箱と床との摩擦抵抗は、接地面積の大きさにはまったく関係しないという事です。
もしまだそんな事はないと思っている貴方に、衝撃の事実をお教えしましょう。
なんと、貴方が中学校の頃に習った理科の教科書にこう書かれているのです。
物体と物体の摩擦力は、その接触面積にはよらず、荷重に比例する。
そして、摩擦力(F)=摩擦係数(μ)×荷重(P)である。
そして、摩擦力(F)=摩擦係数(μ)×荷重(P)である。
どうです?
これで納得して頂けましたでしょうか?
摩擦力の計算の中に、面積は一切入っていないのです。
これをタイヤに当てはめてみると、誰もがタイヤは太い(接地面積が大きい)方がグリップが良いと思っているのですが、実は全く関係しないという事です。
すなち、タイヤが太くても細くても、グリップ(摩擦力)は全く同じなのです。
だとするとなぜF1をはじめとするハイパフォーマンス車のタイヤが太いかと言うと、細いタイヤだと耐久性が足りないからです。
もう少し詳しく説明しますと、太いタイヤにすると単位面積当たりの荷重が小さくなるので、その分耐久性に優れる(摩耗し難い)という訳です。
ですので、例えばF1カーのタイヤを大きくして接地面積を2倍にすれば耐久性も2倍になるので、タイヤの交換回数を半分に減らす事ができます。

タイヤの接地面積を2倍にすればタイヤの耐久性も2倍になる
ただしそうすると荷重も増え、空気抵抗も増えるので、総合的に判断して一番妥当な大きさに抑えているのです。
例え話を段ボールに戻すと、床と擦った事による段ボール底面へのダメージは、接地面積の広い寝かした場合より、接地面積の狭い立てた場合の方が大きいといえばイメージし易いでしょうか?
3. 摩擦力を測定する
上の記事だけではご納得頂けない方のために、論より証拠で今回は実際に摩擦力を測定してみたいと思います。
先生方もお忙しいのでしょうが、こういう実験を学校で実施しないから、自然科学に関する造詣が失われ、ひいては間違った情報が蔓延する理由だと思うのですが、愚痴はこれくらいにして先に進みます。
摩擦力とは、物体が動くのを妨げる力になりますので、物体を動かすための力と同じ値になります。
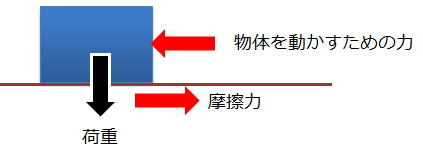
ですので、物体を押して動くときの力を測定すれば、摩擦力が求められます。
なお止まっている物体を動かす場合を静摩擦力、動いている場合を動摩擦力と呼び、通常静摩擦力の方が動摩擦力より大きくなります。
静摩擦力を測定する場合は、押す力のピーク値を測定する必要があるため、本書では動摩擦力を測定する事にします。
なお測定器にピークホールド(押す力の最大値を保持できる)機能があれば、静摩擦力も簡単に測定できます。
4. 実験の準備
それでは実験の準備に取り掛かりましょう。
今回は身近にある木片と木製机の摩擦力を測定してみます。
ですので、用意する物は、木片と重りとテンションゲージ(バネ秤)です。
重りを用意したのは、木片だけだと軽すぎて、用意したテンションゲージでは指針がほとんど触れない場合に備えてです。
先ず木片を平らな面を下にして机の上に置きます。
その上に重りを乗せてテンションゲージで押して、木片が動いているときのテンションゲージの値を読み取ります。
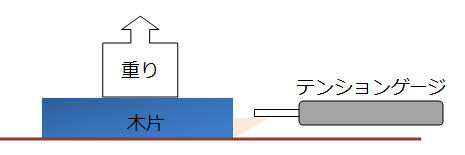
その値が動摩擦力になります。
また用意したテンションゲージは、最大500cN(5N)まで測定できるのですが、力の単位をニュートンにすると少々分かり難いと思いますので、ここでは分かり易い様に最大500gf用のテンションゲージという事にしておきます。

MAX 500cNのテンションゲージ
ですので指針が50を指したら、50gfになります。
なおそう言うと不正確だ、いい加減だという方もいらっしゃると思いますが、そういう方は次をお読み頂ければと思います。
もし興味がなければ、次の5項と6項を飛ばしてして7. 実験開始までお進すみ下さい。
5. テンションゲージとバネ秤の違い
先ほど実験で、テンションゲージ(バネ秤)を用意するとお伝えしましたが、テンションゲージとバネ秤の違いをご存じでしょうか?
テンションゲージとは元々はベルトの張り具合を調整するために、ベルトを所定の強さで押すためのゲージでした。
ですので下の図の場合、矢印の箇所を100Nの力で押して、新品ベルトが3.4~3.8mm撓む様にベルトの張りを調整すれば良い事になります。
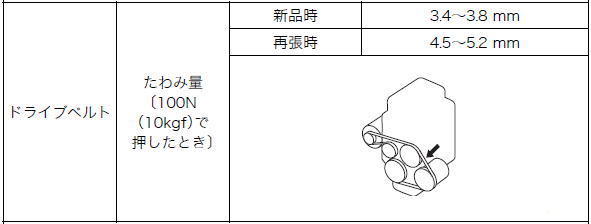
テンションゲージで矢印部を押してベルトの撓み量を測定する
一方バネ秤とは、ご存じの様に質量を測定するものです。
ですので測定単位は、テンションゲージはN(昔はgf)、バネ秤はgになります。
では具体的に、テンションゲージとバネ秤はどう違うのでしょうか?
実は中身は全く同じなのです。
|
テンションゲージ |
|
バネ秤 |
違うのはテンションゲージの場合片側にも棒が飛び出ているのと、目盛の付け方、そしてもう一つ大きな違いがあるのですが、ご存じでしょうか?
もう一つの違いは校正の方法です。
校正の方法と言っても、いずれもトレーサビリティ(国際原器までの校正ルート)のとれた重り(分銅)を測定して、測定器の規格内かどうか確認するだけの話なのですが、使う重りが異なります。
バネ秤はグラム単位の重りを使い、テンションゲージはニュートン単位の重りを使うのです。
こんな事を知っている人はそんなにいないと思いますので、覚えておいて損はありません。
6. センチニュートンはグラムと同じ
さて、以上を知って頂いた上でようやく本題です。
先ほど、今回使ったテンションゲージは最大500cN(5N)まで測定できるとお伝えしました。

cNとはどういう意味だ?
このcN(センチニュートン)ですが、何とも分かり難い(ピンとこない)単位だと思いませんか。
センチとは1/100の単位ですので、100cN=1Nになります。
ですので、500cNは5Nなので、初めから5Nと書けば済む話です。
なぜテンションゲージには、cN(センチニュートン)と分かり難い単位が使われているのでしょうか?
ちなみにトルクゲージにもcN・mという単位が見られます。

トルクゲージの単位にもcN・mが使われている
それは、1N≒0.1kgf(正確には0.10207kgf)だからなのです。
その理由は以下の通りです。
先ず1Nとは、1kgの物質に1m/s2 の加速度を生じさせる力と定義されています。
一方、地球上であらゆる物質に掛かる重力加速度は9.8m/s2です。
ですので、当然ながら地球上で1kgの物質に掛かる重力加速度も9.8m/s2です。
という事は、1kgを9.8で割った0.102kgであれば、地球上で1Nの力を生じさせる事ができます。
これを言い換えると、先ほどお伝えした1N≒0.1kgf(正確には0.10207kgf)になると言う訳です。
さらに、100cN=1N≒0.1kgf=100gfとなるので、100cN≒(昔から良く知っている)100gfとなるのです。
ではここで、バネ秤とテンションゲージの目盛の違いを見ておきましょう。
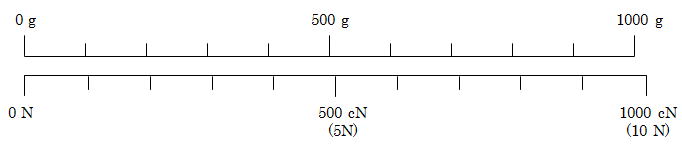
上の図をご覧頂きます様に、両者には2%ほどの差があるのですが、それほど大きな差は無いとも言えます。
ですので、早い話が500cNのテンションゲージは、500gのバネ秤だと思えば良いのです。
ただし、これは余り大声で言えない話ですので、ここだけの話にしておいて下さい。
失敗談
と言いながら、先日これに関連して大失敗をしてしまいましたので、お伝えしておきます。
ご存じないかもしれませんが、定形外郵便物はの送料は500g以下が500円、500gを超えると700円になります。
このため、テンションゲージで測ってぎりぎり500cN以下に梱包した品物を郵便局に持って行った所、何と郵便局の電子天秤では500gを超えてしまいました。
不思議に思いながらも、しぶしぶ700円払って発送したのですが、後で考えたらこの2%の差が効いていた様です。
お金の絡んだ測定においては、この差を忘れてはいけません。
7. 実験開始
それでは実験開始です。
下の写真の様に木片を平らに置いた場合の押す力(動かす力)は、50gfでした。

平らに置いた木片の摩擦力は50gfだった
ですので、この場合の摩擦力は50gfです。
ここでもまた脱線させて下さい。
この様な実験を行うと、恐らく殆どの方が摩擦力は約50gfでした、と書かれると思います。
それが間違いだとは言いませんが、ここは50gfと書くべきです。
当然何度か同じ実験を繰り返せば、40gfのときがあれば、60gfのときもあります。
特に摩擦力の試験は、バラつきが大きくなります。
その様な場合は、平均して50gfとし、更にこのゲージの分解能(最少目盛単位)は10gfですので、約を付けずに摩擦力は50gfと書くのが正しい実験数値の書き方なのです。
人が作った金額と異なり、自然界にはぴったりの数値は存在しないので、これに約を付けたら、あらゆる測定値に約を付けなければなりません。
なかなか前に進みませんが、それでは次に木片を立てて押してみます。
はたして50gf以下になるでしょうか?
すると木片を平らに置いた時と同じ様に、押す力(摩擦力)は50gfでした。

立てて置いた木片の摩擦力も50gfだった
少々見難いですが、上の写真のテンションゲージが50gfを指しているのが分かって頂けると思います。
木片の大きさは、94mmx63mmx15mmですので、平らにしたとき(接地面積:5922mm2)と横にした時(接地面積:1410)では、接地面積は4倍以上も異なります。
にも関わらず摩擦力は同じなのです。
これで物体と物体の摩擦力は、その接触面積にはよらないというのを、十分ご理解頂けたのではないでしょうか。
面積が4倍になっても摩擦力は変わらないのに、タイヤの幅をほんの数十mm広げてグリップが良くなるというのは、正に笑止千万、荒唐無稽の話です。
8. 摩擦係数を求める
今回摩擦力が分かったので、折角ですから摩擦係数も求めてみたいと思います。
先にお伝えしました様に摩擦力は以下の式で求められます。
摩擦力(F)=摩擦係数(μ)×荷重(P)
ですので、摩擦係数は以下の式で求められます。
摩擦係数(μ)=摩擦力(F)÷荷重(P)
求める式が分かった所で、またまた問題です。
摩擦係数の単位は何でしょうか?
摩擦力がkgfで荷重がkgだとすると、kgf/kgと思われるかもしれませんが、違います。
詳しくはこちらをご覧頂くとして、荷重の単位も実はkgfなのです。
単位にkgを使うのは、日本語の場合、質量と重量だけで、その他の重さや荷重の単位は全てkgfなのです。
この場合、摩擦力も荷重も単位は同じkgfですので、摩擦係数には単位が無いのです。
そこまで分かれば、摩擦係数を求めるのは簡単です。
木片と重りの重さを一緒に測れば、荷重が分かります。
同じテンションゲージを使って測ったら、280gfでした。
これを前述の式に入れてやれば、以下の様になります。
| 摩擦係数(μ) | = | 摩擦力(F)÷荷重(P) |
| = | 50gf÷280gf | |
| = | 0.18 |
という訳で、木と机の間の摩擦係数は0.18と求められました。
一般的に木と木の摩擦係数は0.2~0.5程度と言われていますが、使用した机には表面にコーティング処理さていますので、それより小さい値になったと推測されます。
9. 摩擦とは何か?
ここまで分かってくると摩擦の正体を知りたいと思いませんか?
現在は二つの要素が考えられています。
アンカー効果(機械的結合)
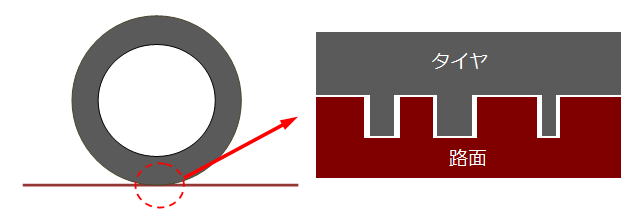
一つ目は、誰でも思い付く物体表面のデコボコの食い込みです。
タイヤの場合でしたら、タイヤのゴムが路面の細かいデコボコに食い込んで、抵抗になると考えれば分かり易いと思います。
分子間引力(物理的結合)
そして二つ目が、分子間引力です。
引力と聞くと、リンゴに掛かる地球の引力とか、潮の満ち引きに影響する月の引力等を思い浮かべてしまいますが、実はあらゆる物体の間で引力は働いているのです。

引力は天体間だけでなく全ての物体間で働いている
ただし地球の引力に比べて余りに小さいので、普段はそれを感じる事はできません。
ところが、以下の引力の式に示す様に、二つの物体の距離が限りなくゼロに近付くと、この引力はとてつもなく大きな値になるのです。
引力=定数 x 物体Aの質量 x 物体Bの質量 ÷ 二つの距離の二乗
そうは言っても、コーヒーカップが下に敷いたソーサーに張り付いたりする事はありません。

コーヒーカップはソーサーに張り付かない
これはコーヒーカップの底がソーサーに接触している様に見えても、実は接触面はでこぼで所々が点で接触しているだけなので、ミクロ的に見れば実際は浮いている様なものだからです。
ところが、この物体間の引力を実際に認識できる場面があります。
それがブロックゲージです。
ご存じの方は少ないと思いますが、ブロックゲージとは長さの基準となる、固い金属もしくはセラミックのブロックを指します。

ブロックゲージのセット
このブロックゲージの表面は、寸法の基準になるため、真っ平らで且つピカピカに磨かれています。
この真っ平らでピカピカに磨かれた二つのブロックゲージの表面同士を強く押し当てて擦り付けると、あら不思議。
見事にくっついてしまうのです。
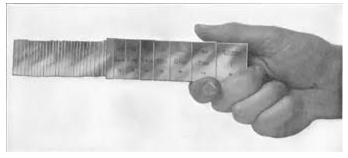
見事にくっついた数十個のブロックゲージ
この現象はリンギングと呼ばれていますが、これはブロックゲージ同士が分子レベルで接近した事による引力によるものと考えられています。
生憎この現象の摩擦への寄与度はどれくらいかは不明ですが、タイヤの場合でしたら、タイヤが路面に強く接触して隙間が小さくなればなるほど、この引力も増えていくという訳です。
またタイヤが高温になってベトベトしてくると、グリップが良くなるのは、同じ様にこの分子間引力が増大したせいと考えられます。
話が長ーくなってしまいましたが、摩擦とはデコボコの食い込みと、この分子間引力が2大要因と考えられています。
10. 給紙ローラー
さてここまで読んで頂いても、なお太いタイヤの方がグリップは良いと頑なに思われている方は間違いなくいらっしゃる事でしょう。
そういう方は、木片はそうなるかもしれないが、ゴムと舗装路なら違うと言い張るのかもしれません。
或いは、木片の摩擦力は滑り摩擦で、タイヤの場合の転がり摩擦とは違うと言われるのかもしれません。
転がり摩擦は滑り摩擦より小さくなる
ですが、相手がゴムであろうと、転がり摩擦だろうと、事態は何も変わらないのです。
そういう方のために、次に給紙ローラーの話をしたいと思います。
給紙ローラーとは、複写機やプリンターに付いている、用紙を1枚ずつ機内に取り込むゴムローラの事です。

プリンターの給紙口から機内を覗くと、これが見えると思います。
最近はコストダウンで、1個だけ付いている機械が多くなってきましたが、その昔は以下の様に複数付いているのが一般的でした。
用紙カセットと給紙ローラー
これが劣化して滑り出すと、紙を給紙できなくてジャムが発生するという訳です。
ただしゴムの劣化が無くても、厚紙になると用紙が重くなり、やはり給紙不良が発生する事になります。
その昔どうしても厚紙を通紙したくて、メーカーから給紙ローラを取り寄せて、シャフトに追加してみた事があります。
その結果、どうなったと思われるでしょう。
誰しも給紙ローラー2個よりも4個になった方が、給紙性能は上がると思われるでしょう。
当時は本書も同じでした。
とろが全く変わらないのです。
4個にしても6個にしても、はたまた8個にしても事態は全く変わらないのです。
すなわち、給紙ローラをいくつ増やしても給紙性能は全く変わらない(摩擦力は全く増えない)のです。
当時は不思議でしょうがなかったのですが、今にしたら当前の事です。
なぜならば、摩擦力は接触面積には関係しないからです。
もし摩擦力を増やしたいのならば、用紙カセットの底に付いているバネを強くして、紙と給紙ローラの接触圧(荷重)を上げるしかないのです。
これはゴムと紙との関係で、尚且つ動くのは紙の方ですが、ゴムと路面の間で異なる事が起こる訳がありません。
すなわちクルマのタイヤを太くしても、グリップが良くなる事など決してないのです。
本書がタイヤは太くなってもグリップは変わらないと、自信を持って断言できるのも、実はこの経験があるからこそなのです。
11. なぜ摩擦力は接触面積に関係しないのか?
それでは次に、なぜ摩擦力は接触面積に関係しないのか、について考えてみたいと思います。
これも実に簡単です。
例えばここに総重量1000kgのクルマが1台あって、タイヤが4本付いていたとします。
としますと、タイヤ1本に掛かる荷重は250kgfです。
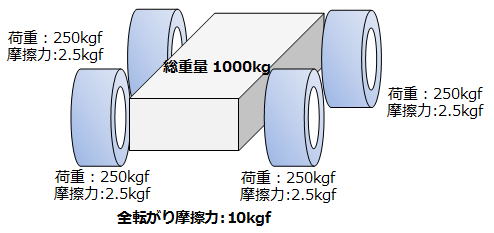
計算を簡単にするためにタイヤと路面との転がり摩擦係数を0.01だとすると、1本当たりの摩擦力は2.5kgfになり、全摩擦力は2.5kgfの4倍で10kgfになります。
次にこのクルマに総重量を変えないで、全てのタイヤをダブルで装着してみましょう。
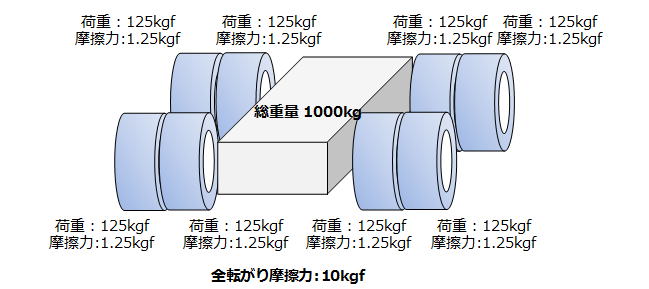
そうすると1本のタイヤに掛かる荷重は、半分の125kgfになります。
そうなると1本当たりの摩擦力も、半分の1.25kgfになってしまいます。
このため、全摩擦力は1.25kgf の8倍で、やはり10kgfと同じになるという訳です。
何が言いたいかと言えば、接触面積が増えても、単位面積当たりの荷重が減るので、トータルでの摩擦力は変わらないのです。
これほど矛盾のない単純明快な理論なのに、何故タイヤが太くなればグリップが良くなると考えるのでしょうか?
おっと。言い忘れていましたが、ここで一つ重要な事があります。
ここではダブルタイヤにしても、総重量は同じ1000kgという事にしています。
ですが、もしダブルタイヤにして重量がタイヤ4本分増えたとしたら、ダブルタイヤの方がグリップが良くなります。
ただしこれはタイヤが太くなったからではなく、タイヤ4本分重くなったためで、シングルタイヤのクルマにタイヤを4本乗せた場合と同じグリップになります。
12. タイヤの空気圧が高いとなぜ走行抵抗は少なくなるのか?
これでタイヤが太くなってもグリップが良くならないとかなり信じて頂けたと思うのですが、念のためにこの話もしておきましょう。
実は本書の読者より、以下のお便りを頂きました。
タイヤは太い程グリップは良くなる筈だ。
なぜならば、
①タイヤの空気圧が低いと、タイヤの接地面積は大きくなる。
確かにその通りです。
②そしてタイヤの空気圧が低いほど、走行抵抗は大きくなる。
これもその通りで、確かにタイヤの空気圧を下げると、乗り心地は良くなるものの、明らかに燃費は悪化します。
③故に接地面積が増えれば、摩擦力が増えグリップは良くなる筈だ。
なぜならば、
①タイヤの空気圧が低いと、タイヤの接地面積は大きくなる。
確かにその通りです。
②そしてタイヤの空気圧が低いほど、走行抵抗は大きくなる。
これもその通りで、確かにタイヤの空気圧を下げると、乗り心地は良くなるものの、明らかに燃費は悪化します。
③故に接地面積が増えれば、摩擦力が増えグリップは良くなる筈だ。
いかがでしょう。
見事な3段論法で一見正しい様に思うのですが、一か所間違いがあります。
それは②から③に話が移行する所です。
もしタイヤの走行抵抗が路面からの摩擦力だけでしたら、この理論は正しいのですが、残念ながらタイヤの走行抵抗には他に2つの要因があるのです。
下の図は日本自動車タイヤ協会作成資料ですが、これをご覧頂きます様にタイヤが受ける抵抗は路面からの②摩擦力(接地摩擦)だけではなく、①タイヤ変形と③空気抵抗があるのです。
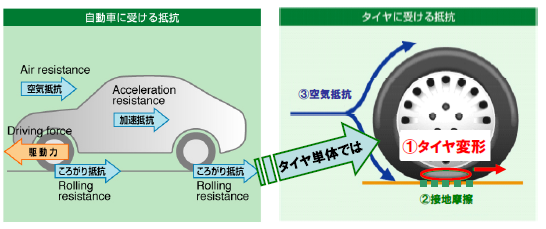
日本自動車タイヤ協会作成資料
空気抵抗についてはタイヤの空気圧の違いでは無視できるとして、空気の抜けたタイヤによって走行抵抗が増えたのは、タイヤの摩擦力が大きくなったためではなく、タイヤの変形量が大きくなり、それによって走行抵抗が増えてしまったためなのです。
空気が抜けたタイヤの側面を見ると、地面と接触する部分は縮み、そこから離れると膨らみますので、走行中常に伸びたり縮んだりを繰り返している事になります。
これによって駆動力の一部をタイヤの発熱に消耗してしまっているという訳です。
タイヤ変形については次のタイヤの話Ⅱでまたお話しますが、一応ここにも載せておきます。
13. グリップが良くなると走行性能が上がる?
タイヤを太くするとグリップが上がると主張するサイトを見ると、これによって、走る、止まる、曲がるの全てが良くなると書かれています。
確かにタイヤのグリップが良くなれば、止まる、曲がるについては良くなります。
しかし走行性能が上がるというのは、真っ赤なウソです。
何故ならば、グリップが上がるという事は、走行抵抗が増えるという事ですから、間違いなく走行性能は落ちます。
これは空気抵抗が増えるから、走行性能は上がると言うのと同じ事です。
確かにホイールスピンをしながら加速する様な場合でしたら、グリップが良ければその分路面との滑りが無くなりますので、瞬間的には加速は良くなるかもしれません。
ですがそれ以降は、グリップが大きいと常時路面からの抵抗が大きいのですから、いつかどこかでグリップの小さいタイヤに抜かれる事になるのです。
当然ながら最高速についても、グリップの良いクルマの方が遅いのです。
当然の事です。
14. 太いタイヤのデメリット
ここまで読んで頂ければ、さすがに太いタイヤの方がグリップが良いという認識は薄らいできたと思うのですが、ついでにタイヤを太くした場合のデメリットをお伝えしておきましょう。
先ほどタイヤをダブルにした場合、1本当たりに掛かる荷重が半分になるとお伝えしました。
これでどんな弊害があるかと言えば、雨の日に滑り易くなるのです。
ご存じの通り雨の日にタイヤが滑り易くなるのは、路面とタイヤの間に水の膜ができるためですが、接地荷重が半分になると、水の膜を切り裂いて路面と接触する力が弱くなるため、更に滑り易くなるのです。
万一タイヤを太くしたら、間違いなく雨の日に滑り易くなりますので、それ以前と同じ様に走ったらかなり危険です。
もっと顕著なのは、雪の日です。
太いタイヤのままで雪の日に出かけるのは、雪山に遭難しに行く様なものです。
折角高いお金を払ってタイヤを太くしても、重くなるし、空気抵抗も増えるし、燃費も悪くなるし、雨の日や雪の日は危険度が増すにも関わらず、グリップは何一つ変わらないのです。
唯一の長所は、僅かながら耐久性が増す事ぐらいでしょう。
なぜ太いタイヤに換えるのでしょうか?
15. まとめ
いかがでしょうか?
これでもまだ太いタイヤはグリップが良くなるとお考えでしょうか?
もしまだそう思われる方がいらっしゃいましたら、是非ご自分で実験してみて頂きたいと思います。
例えば、以下の様な事を実施して頂ければ、立ち所に明確になると思います。
①同じカーブを高速で曲がってみて、滑り始めの速度はそれぞれ時速何kmだったか。
②同じ速度でブレーキを踏んでみて、どちらがより短い距離で停止できたか。
③同じ速度でギアをニュートラルに入れて、どちらがより遠くまで進んだか。
④同じサーキットを走って、どちらが速かったか?
本サイトにも、たまに太いタイヤの方がグリップが良くなるとのメールを頂きます。
ですがその理由に、昔から色々なクルマを乗り継いできたから、或いはサーキットで運転した事があるからと書かれても、何の説得力もありません。
今から50年ほど前でしたら、外車に乗った事がある、サーキットを運転した事がある、A級ライセンスを持っていると聞いただけで、いい加減な事でも簡単に信じてしまいましたが、今時そんな事は自慢にすらなりません。
タイヤが太くなってもグリップは変わらない。
これが真実です。
16. なぜタイヤメーカーは黙っているのか?
まとめの後で恐縮ですが、最後にこれについても触れておきたいと思います。
海外を含めてですが、ネットを検索すると、このタイヤの太さとグリップについては同じ様に意見が分かれている様です。
ですが不思議なのは、(本サイトが調べる限り)タイヤメーカーは本件に関して一切オフィシャルなコメントを出していません。
なぜなのでしょうか?
これには二つのケースが考えられます。
一つは、太いタイヤの方がグリップが良いのはあまりにも当然だから。
もう一つは、太いタイヤにしてもグリップは全く変わらないのだが、積極的にそれを公表すると、誤解して太いタイヤに買い換えて貰えなくなるから。
はたしてどちらが真相でしょうか?
ついでに言えば、(本サイトが調べる限り)どのタイヤメーカーにおいても、太いタイヤへの履き替えを勧める広告は一切出していません。
ちなみにタイヤの対応リム幅は、2インチほどの余裕がありますので、20mm程度タイヤを太くするのでしたら、今のホイールをそのまま使用できます。
にも関わらず太いタイヤを勧めないという事は、これこそタイヤメーカーの良心ではないでしょうか。
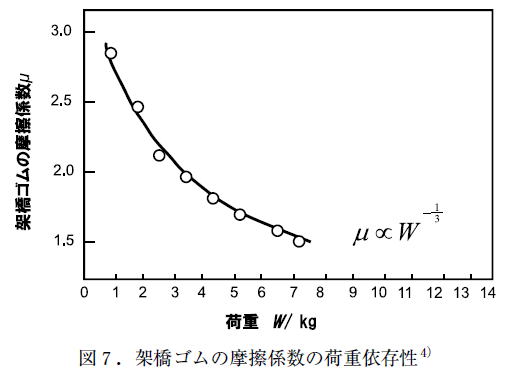
17. ゴムの摩擦係数は変化する?
その後読者の方より、衝撃的な情報を頂きました。
それによると、ゴムの様な弾性体の場合、摩擦係数は荷重の-1/3乗に比例するという、日本ゴム協会が発行した記事があるとの事です。
確かに上の(試験結果に基づいたと思われる)チャートを見ると、明らかにその傾向が見られます。
そう言えば以前読者の方より、ゴムの摩擦係数は一定ではないとか、最近の研究では荷重が大きくなると摩擦係数が低下する傾向が分かってきた、とのメールを頂いた事があります。
当時頂いたメールにはそれ以上の事は書かれていなかったのですが、もしかしたらこの記事が基になっていたのかもしれません。
それはともかく、もしこれが事実ならば、本サイトの主張が根本的に覆される事になります。
果たして、真相はどちらなのでしょうか?
本件については、こちらにアップしましたので、興味のある方は覗いてみて頂ければ幸甚です。
常識を覆すタイヤの太さとグリップの関係
(タイヤを太くしてもグリップは変わらない)
(タイヤを太くしてもグリップは変わらない)
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/3e0c5293.8c7a535e.3e0c5294.987827cd/?me_id=1198680&item_id=10702732&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Ftuzukiya%2Fcabinet%2F0%2F0%2F6588%2Fn77-0112.jpg%3F_ex%3D240x240&s=240x240&t=picttext)

![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/3e0c58e7.78fa9d33.3e0c58e8.3c36eaca/?me_id=1298559&item_id=10056906&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fchubonotakumi%2Fcabinet%2Fhg04-0469%2Fk-605462.jpg%3F_ex%3D128x128&s=128x128&t=picttext)