(再検証しても変わらなかった)
タイヤを太くしてもグリップは変わらない
2018/6: 発行
目次
1. はじめに
本サイトではこれまで、タイヤが太くなってもグリップは変わらないと一貫して主張していたのですが、この度読者の方より興味深い(衝撃的な)情報を頂きました。
それは弾性のあるゴムの場合、摩擦係数は荷重の-1/3乗に比例するというものです。
という事は、接地面積が同じであれば、荷重が小さいほど摩擦係数は高いという事です。
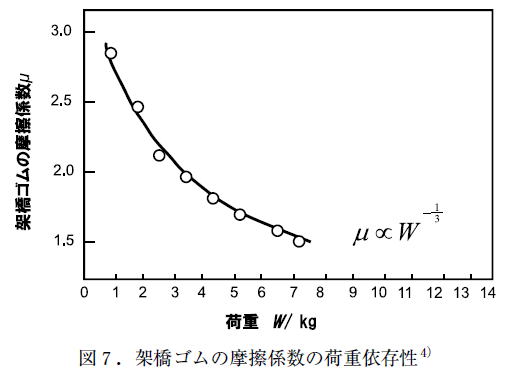
以下のチャートは、日本ゴム協会(一般社団法人)会誌の”やさしいゴムの物理”から抜粋したものです。
このチャートを見ると、確かにその傾向が見られます。
となると、もしかしたら太いタイヤほどグリップが良くなるかもしれないという、由々しき事態です。
という訳で、早速真実を探ってみたいと思います。
2. 摩擦係数が一定の場合
それでは先ず、旧来の考え方(荷重によって摩擦係数が変化しない)において、なぜタイヤが太くなってもグリップが変わらないかについて考えてみたいと思います。
単純に考えると、タイヤが太くなればその分接地面積が増えるので、摩擦力は増える様な気がしますが、実はそうではありません。
下の図は、タイヤの接地面積が2倍になった場合の、単位面積当たりの荷重と摩擦力の関係を示しています。
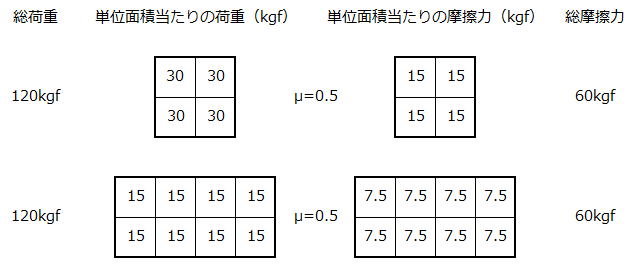
少々分かり難いかもしれませんが、上段が接地面識が小さい場合で、下段が2倍に大きくなった場合を表しています。
すなわち上段が元々のタイヤの大きさで、下段がタイヤを2倍に太くした場合という訳です。
上段において、1本のタイヤに掛かる荷重が120kgfで、タイヤの摩擦係数が0.5だとすると、単位面積当たりの荷重は30kgfで、そのときの単位面積当たりの摩擦力(荷重×摩擦係数)は15kgfとなり、全部で60kgfになります。
次に下段の場合で、もしタイヤの接地面積が2倍になったとすると、単位面積当たりの荷重も半分の15kgfになり、これに伴って単位面積当たりの摩擦力も半分の7.5kgfになります。
ただし、接地面積は2倍なるので、単位面積当たりの摩擦力を全部足した総摩擦力は上段と同じ60kgfになるという訳です。
早い話が、接地面積が増えても総摩擦力は変わらないという(いつもの)話なのですが、何故こんなに回りくどい話をしたかと言えば、次の説明に繋げるためです。
ここまでは問題ないでしょうか。
3. 摩擦係数が荷重によって変化する場合
それでは次に、摩擦係数が荷重の-1/3乗に比例する場合を考えてみます。
安直に考えると、接地面積が増えても、総荷重が同じならば、総摩擦力は変わらないと思ってしまいますが、実は変わります。
下の図は、先程と同じ様にタイヤの接地面積が2倍になった場合の、単位面積当たりの荷重と摩擦力の関係を示しています。
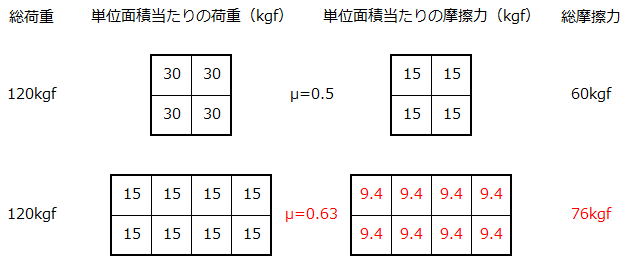
ただし、摩擦係数が荷重の-1/3乗で変わる事から、下段の摩擦係数と摩擦力が増えています。
上段については、先の説明図と同じなので飛ばすとして、問題は下段です。
この場合、単位面積当たりの荷重が30kgfから15kgfに低下する事により、摩擦係数は以下の式により1.26倍にアップする事になります。
単位面積当たりの荷重が半分になった場合の摩擦係数の変化率=(1/2) ^ (-1/3) = 1.26
元の摩擦係数が0.5なので、これを1.26倍して摩擦係数が0.63にアップします。
これに伴って、単位面積当たりの摩擦力が9.4kgfになり、結果的に総摩擦力は76kgfになります。
これをまとめると、接地面積が2倍になると、単位面積当たりの荷重は半分になり、それに伴って摩擦係数は1.26倍になり、総摩擦力も1.26倍になるという事です。
このため、タイヤが太くなれば、グリップが上がる事になります。
4. 検証1
それではこの理論が本当にタイヤにも当てはまるのかどうか、検証してみたいと思います。
使用するデータは、以前弊サイトで使用しました車両重量と制動距離のデータです。
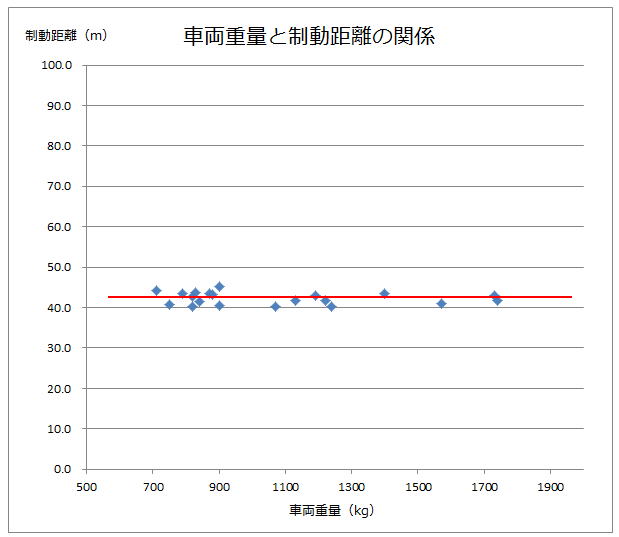
これは国土交通省の制動試験を基に、20台の異なるクルマの、車両重量と制動距離の関係をプロットしたチャートです。
これをご覧頂きます様に、多少のバラツキはあるものの、制動距離は車両重量に関わらず一定である事が分かります。
詳細はこちらをお読み頂くとして、これはすなわち、摩擦係数は車両重量に関わらず一定という事を表しています。
もし車両重量が増えると摩擦係数が小さくなるのでしたら、赤い線は右肩上がりになる筈です。
具体的にどれくらい制動距離が伸びるかと言えば、このチャートの中で一番軽いクルマがダイハツ・エッセの710㎏で、一番重いのがトヨタ・エスティマの1740㎏です。
という事は、両者の重量差は倍率で2.5倍です。
2.5の-1/3乗は0.74(=2.5 ^ (-1/3) )ですので、仮にエッセの摩擦係数が0.9だとするとエスティマの摩擦系素は0.67(=0.74×0.9)に低下します。
制動距離が以下の式で求められるとすると、エスティマの制動距離は58mにもなってしまいます。
| L | =v2/2μg |
| =(27.8 m/s)2/(2x0.67x9.8m/s2) | |
| =58m |
実際のエスティマの制動距離は41.7mなので、どうみても辻褄が合いません。
ですのでこの理論はタイヤには当てはまらないと断言して、これで終わりにしたいのですが、実はまだ先があります。
5. 検証2
先程、車両重量が増えると摩擦係数が小さくなるとしたら、赤い線は右肩上がりになる筈だとお伝えしました。
ですが、それは両車のタイヤサイズが同じ場合です。
当然ながら重いクルマのタイヤは軽いクルマより大きいので、接地面積も大きくなります。
このため、車両重量が増えて摩擦係数が小さくなっても、タイヤも大きくなって(単位面積当たりの荷重も小さくなって)摩擦係数が大きくなる事で、両者がお互いに打ち消し合って、制動距離が変わらない場合も考えられます。
という訳で、この理屈が当たっているかどうか、先ほど登場したダイハツ・エッセとトヨタ・エスティマで調べてみます。
タイヤの接地面積は、タイヤの横幅と接地長さを掛ければ求められます。
タイヤの横幅はサイズ表から分かりますが、接地長さは不明です。
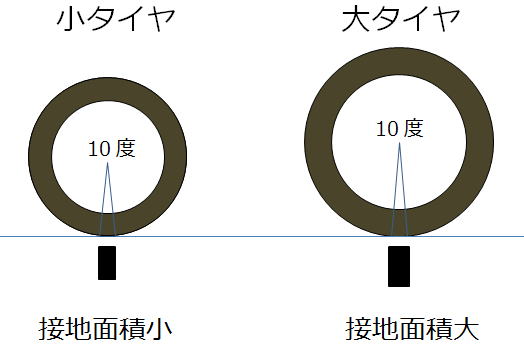
このため上の図の様に、接地長さはタイヤの中心からの角度10度の弦の長さと仮定して計算してみます。
この10度の弦の長さが適切かどうかは甚だ疑問なのですが、あくまでも比較用と割り切ればそれほど大きな間違いとは言えないだろうという訳です。
ちなみに弦の長さは以下の式から求められます。
弦の長さ=直径×sin (角度/2)
ダイハツ・エッセのタイヤサイズが145/80R12で、外径が536mmなので接地長さは以下の様に47mmなります。
| エッセ接地長さ | =536mmxsin 5° |
| =536mm x 0.087 | |
| =47mm |
ですので、接地面積は47mm×145mmで68cm² になります。
次にトヨタ・エスティマのタイヤサイズは215/55R17 ですので、接地長さは58mmになります。
| エスティマ接地長さ | =668mmxsin 5° |
| =668mm x 0.087 | |
| =58mm |
そして接地面積は58mm×215mmで125cm² になり、エッセの1.8倍になります。
という事は、もし2台の車両重量が同じであれば、エスティマの単位面積当たりの荷重はエッセの0.56倍(=1/1.8)になります。
ただし車両重量が2.5倍違いますので、最終的にエスティマの単位面積当たりの荷重はエッセの1.4倍(2.5×0.56)になり、摩擦係数は0.89倍(=1.4^ (-1/3) )になります。
だとすると、前項と同じようにエスティマの制動距離を計算すると49m(実測値は41.7m)になります。
いくつか仮説を元にした計算値ですので、しょせん実測値とピッタリ同じ値が出る訳もありませんが、荷重の-1/3乗で摩擦係数が変化するというのは少々無理がある様に思います。
それより摩擦係数は一定だと考えた方が、実測値とぴったり整合します。
ただし恐らくこの程度の差でしたら、太いタイヤほどグリップが良いと信じている方には、何の説得力もないのかもしれません。
という訳で次に進みます。
6. 検証3
となったら、今まで見ていた車両重量と制動距離のチャートを、試しに単位面積当たりの荷重と制動距離に変換したものを見たくはないでしょうか。
それでもし右肩上がりでしたら、摩擦係数は荷重によって変化すると言えます。
だったら最初からそれを見せろと言われそうですが、下がそのチャートです。
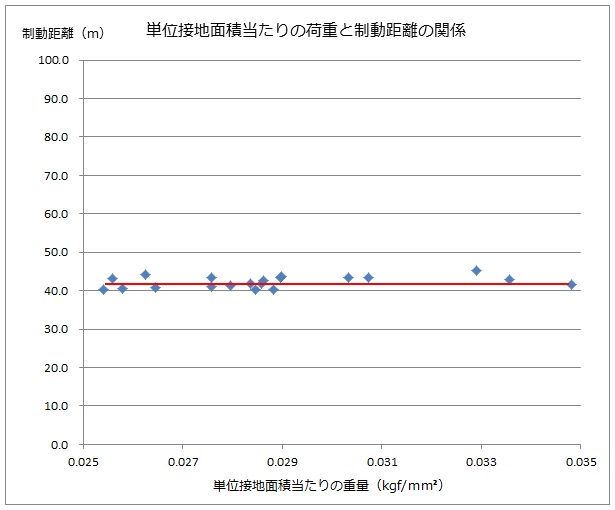
ご覧の様に見事に右肩上がりになりましたと言いたい所ですが、タイトルとX軸の項目名が変わった以外、殆ど代わり映えのしないチャートになります。
本当に変換したのを分かって頂くために、制動距離43m部分を拡大して、車種名を載せると以下の様になります。
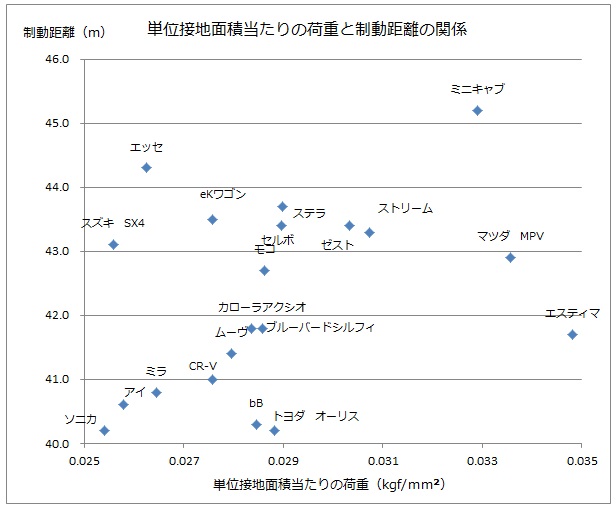
ちなみに変換前が以下のチャートです。
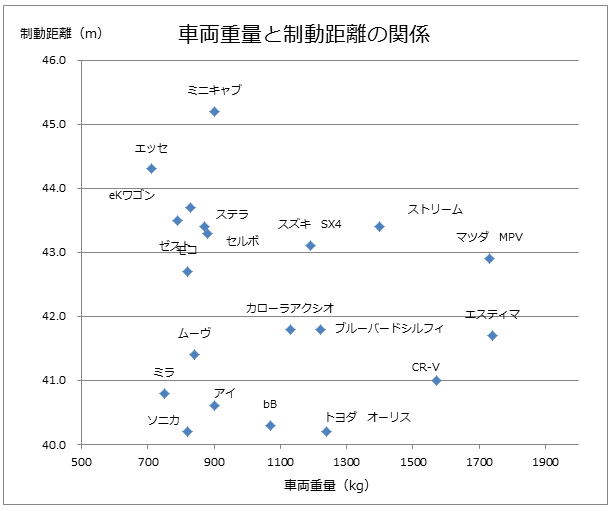
これを見比べて頂きます様に、ミニキャブは車重の割に小さなタイヤを履いているのが分かります。
それはともかく、単位面積当たりの荷重と制動距離の関係においても、右肩上がりの傾向は見られないのは間違いありません。
すなわちクルマの制動距離を見る限り、荷重によって摩擦係数が低下する傾向は全く見られないで、一定という事です。
7. あのチャートの信憑(しんぴょう)性
さて、今までは劣勢に立たされていた本サイトですが、少なくとも制動距離を基に検証すれば、摩擦係数は一定である事を立証できた事から、これからは反転攻勢に打って出ます。
と言っても、ゴム協会の記事を完全に否定する気は毛頭ありません。
もしかしたらある限られた理想的な条件においては、記事の内容に似た現象が起こるのかもしれません。
実際当該記事の初めと終わりには、”ここではゴムの摩擦に関して理想モデルを想定して解説しています”と述べられています。
だとしても、かなり誤解を与える部分もあります。
それが既にお見せした、下のチャートです。
このチャートは分かり易い分、非常にインパクトがありますので、これを一目見れば、誰もがゴムの場合荷重が増えれば摩擦係数が小さくなると信じきってしまうと思います。
おまけに丸いドットがそれらしい間隔でプロットされていますので、間違いなく実験した結果だと思う事でしょう。
ですが、一度でもゴムの摩擦実験をやられた方でしたら、このチャートを一目見るなり、こんなにも美しい曲線を描くなんて有り得ないと思うのは間違いありません。
何故ならば、ゴムの摩擦力の測定はとてつもなくバラツクからです。
もっと言わせて頂けるのでしたら、このチャートはどう見ても作り物としか思えません。
そう思ってこのチャートの説明を読むと、下の様な気になる表現があります。
| 実際にゴムの荷重依存性を実験的に調べた結果を図7に示します。 |
|---|
”実験的に調べた結果”とは、かなり意味深長な言い回しではないでしょうか?
もし実際に実験した結果ならば、以下の様に書くでしょう。
| 実際にゴムの荷重依存性を実験した結果を図7に示します。 |
|---|
この文章の真意はともかくとしても、”実験的に調べた結果”というのは、日本語としてもおかしいですし、技術文章としても明らかに不適切なのは間違いありません。
またこのチャート自体は、別の参考文献(Grosch, K.A.: Proc. Roy. Soc. A, 274, 21(1963))からの引用の様ですが、ネット検索では見つける事はできませんでした。
このチャートは本当に実験結果なのでしょうか?
もしそうだとしたら、どんな試験条件で行われたのでしょうか?
8. 実際の試験結果
さて、先程はチャートの信ぴょう性について述べましたが、次にゴムの場合、本当に荷重が増えると摩擦係数が小さくなるのかどうかを調べてみたいと思います。
これについてもネットでも見られる研究論文(ゴムの摩擦挙動および摩擦試験法に関する研究)を読者の方に提供して頂きましたので、これを元に調べてみたいと思います。
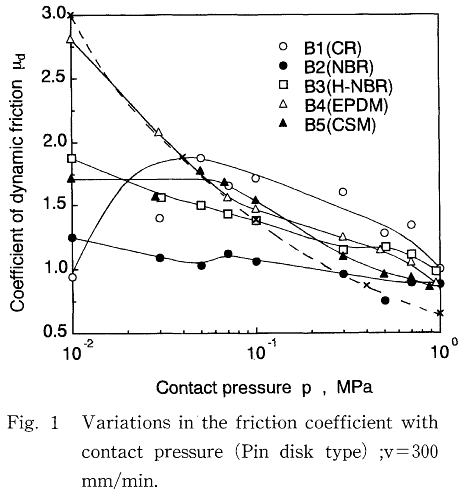
下のチャートは、上記論文に記載されています試験結果の一つで、摩擦係数が比較的右肩下がりの傾向を示しているものです。
これをご覧頂きます様に、摩擦係数は理論通りの-1/3乗のライン(破線)にキレイに沿わずに、そこそバラツイテいるのが分かります。
ただしいずれも、圧力(単位面積当たりの荷重)が増えると、摩擦係数が低下する傾向は見られます。
何だやっぱり、タイヤが太くなるとグリップが良くなる、と思うのは早計です。
これには試験方法や試験条件が詳しく載っていますので、この結果がタイヤにも当てはまるのかどうか調べてみます。
ゴムの種類
先ずは試験されたゴムの種類です。
この試験においてはCR、NBR、H-NBR等、5種類のゴムが使われていますが、タイヤに使われているゴムはどれかご存じでしょうか?
一般的にタイヤに使われているゴムは,、スチレンブタジエンゴム(SBR)なのですが、この試験の中には存在していないのです。
とは言え、他のゴムがどれも右肩下がりの挙動を示すのですから、SBRも恐らく荷重が増えれば摩擦係数は低下するだろうと思って次にいきます。
ちなみに、この論文の関係会社は、バンドー化学、金陽社、ニッタ等なので、タイヤ以外がメインの会社の様です。
次回は是非、ブリジストンや横浜ゴムやダンロップ等のタイヤメーカーを交えて、SBRのデータも載せて頂きたいものです。
と言いながら、その可能性は限りなくゼロである事は、追々分かってくると思います。
ゴムと相手側の摩擦面
次はゴムと相手側の摩擦面の状況です。
実際のタイヤの使用状況と大きく異なるのはここです。
この試験に使われるゴムの摩擦面は、何とCC#1500の研磨紙で磨かれた、ツルツルの表面なのです。
さらに相手側は、ステンレス鋼板で、これまた0.2μm(RA)と呼ばれる顔も映るのではないかと思える程ピカピカの美しい光沢面なのです。
すなわちこの試験結果は、普段私たちが経験する事もないほど滑らかなゴム表面とピカピカの金属面での出来事なのです。
この摩擦面と、タイヤと路面のデコボコの摩擦面が、同じ挙動を示すと思われますでしょうか?
全くそうは思わないのですが、多分同じなんだろうなと無理やり納得して次に進みます。
ただし、タイヤメーカーがタイヤに使うSBRの摩擦係数をこんな風にして測定する事は、まず有り得ないでしょう。
スパン
さて、もっとビックリするのが、このチャートのX軸のスパンです。
対数表示になっていますが、X軸のスパン(幅)は10-2 ~100MPa(すなわち0.01~1MPa)ですので、端から端まで何と100倍もあります。
ところがクルマの場合でしたら、検証3のチャートをご覧頂きます様に、0.025~0.034kgf/mm²とたった1.4倍しかないのです。
ですので、もしタイヤメーカーがこの様な試験を行うとしたら、スパンはせいぜい数倍で、100倍もの荷重など決して掛けないのは間違いありません。
何故ならば、1本のタイヤに掛かる荷重が250kgfだとしたら、100倍ですと25tf(トン重)になり、そのクルマ25台分の荷重を1本のタイヤに掛ける事になるのですから。
早い話が、この試験条件は(同じゴムとは言え)タイヤの摩擦係数を測定するには、全く以て有り得ない条件と言えます。
もっと言わせて頂ければ、この試験結果でタイヤの摩擦を云々する事自体、無謀としか言いようがありません。
そうは言いながらも、このチャートの一部分を抜き出せばタイヤにも適応できるだろうとして、次に進みます。
タイヤにおける摩擦係数の変化量
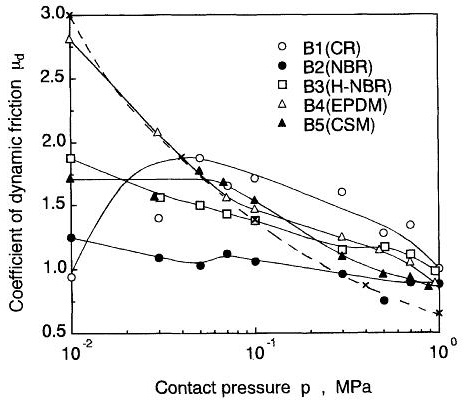
そして先程お伝えした0.025~0.034kgf/mm²をパスカル単位に直すと、0.25~0.34MPaですので、チャート上で関係するのは下の赤い領域だけなのです。
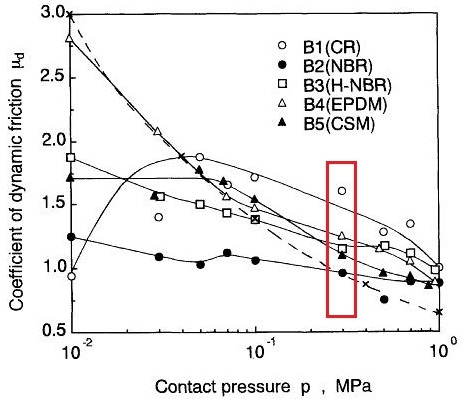
既にお伝えした通り、生憎このチャートの中にはSBRは無いので、どのカーブを見れば良いかは分かりませんが、軽自動車とミニバンほどにタイヤの大きさに差があっても、摩擦係数の差はこの赤枠の範囲内なのです。
また最初にお伝えした様に、上のチャートは比較的右肩下がりの試験結果ですが、別の団体の試験では以下の様にもっと傾斜がなだらかな場合もあるのです。
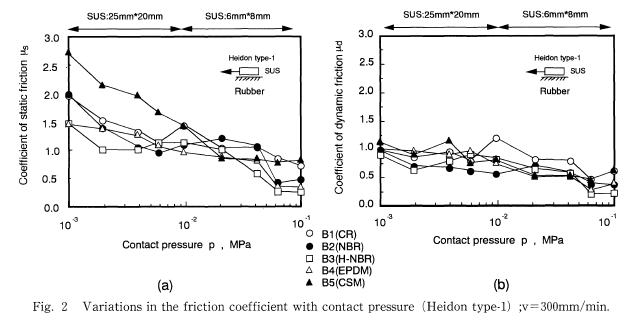
実際、(本書の前半でお伝えした様に)荷重が変わっても制動距離が一定である事を考えれば、仮にタイヤにおいても荷重が大きくなると摩擦係数が低下する傾向があったとしても、その変化量は極めて少ないのは間違いありません。
ましてや、同じクルマのタイヤの幅を数10mm変える程度でしたら、摩擦係数は全く変わらない(一定)と断言しても良いくらいです。
いくら地球が丸いといっても、運動場が球形ではない(平らな)のと同じ理屈です。
という事は、(長々とお読み頂きましたが)従来の説明の通り、タイヤが太くなってもグリップは変わらないという事です。
9. まとめ
それでは最後にまとめです。
①ゴムの摩擦係数は荷重の-1/3乗に比例するという記事があるが、制動距離を基にした検証では、その傾向は全く見られない。
②(タイヤメーカーを除く)ゴムメーカー数社における試験結果においても、ゴムの摩擦係数は荷重が増える事に伴って低下する傾向を示しているが、タイヤの使用状況から大きく乖離した試験方法であり、これがタイヤにも当てはまるかどうか甚(はなは)だ疑問である。
③仮に当該試験結果がタイヤにも当てはまるとしても、タイヤの荷重の変動量からすれば摩擦係数の変動量は極めて微小である。
③よって従来の説明の通り、タイヤを太くしてもグリップ(摩擦力)は変わらない。
こんな結論で、お許し頂けますでしょうか?
再検証:タイヤを太くしてもグリップは変わらない