小学生でも分かるトルクと馬力の話
（本当に早いクルマとは？）

第6章：トルクと加速度の関係
（ニュートンの第2法則を使って、トルクから加速度を求める）

6-1. トルクから加速度を計算する方法

以前馬力を元にクルマのスピードを計算してみましたので、 今度はトルクを元に加速度を計算で求めてみましょう。

加速度を計算で求めるとなると、何やら難しい計算式が出る様に思われるかもしれませんが、実はこの方がもっと簡単なのです。

それこそ、小学生でもできます。

6-2. ニュートンの第2法則

基本の式は、リンゴで有名なニュートンの第2法則です。


上の式が何を意味するかと言うと、リンゴに重力が働いて下に落ちると習ったかもしれませんが、正確にはこうです。



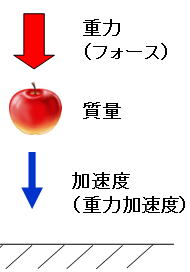
これをもう少し詳しく述べると、上の図にあるリンゴが地面に落ちるのは、リンゴに重力（地面に引力）が掛っているためで、その重力（重さ）はリンゴの質量に加速度（重力加速度）を掛けると求められるという訳です。

ここで質量とは、リンゴの色や形と同じ様なもので、それ自体には重さはありませんが、この質量に加速度が掛って初めて重さが生じるという訳です。

これに気が付いたニュートンは本当にスゴイと思います。

もしこのときニュートンがそれに気が付かなかったら、私たちはまだ農耕生活を送っていたかもしれません。

と普段はこれでオシマイなのですが、この式にはもう一つ別の深い意味があります。


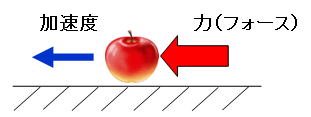
上記はリンゴと重力の垂直な関係でしたが、これを横（水平）にしてリンゴ に力を掛けると、リンゴはどんどん加速しながら転がっていく事を表しています。

リンゴを指で押せば、転がっていくのと同じです。

ただし感覚と少し違うのは、同じスピード（等速）コロコロで転がっていくのではなく、加速しながら転がっている事です。

例えば、リンゴをバネ測りを介して押したとして、バネ測りの指す値を一定にしようとすると、最初はゆっくり歩いていたのに、いつのまにか全力疾走している事で分かって頂けると思います。