小学生でも分かるトルクと馬力の話
(本当に早いクルマとは?)
2016/01: 初版
2016/05: 改訂
2016/05: 改訂
第5章: 走行性能曲線
(走行性能曲線を見れば、そのクルマの走らせ方が分かる)
はじめに
ここでは走行性能曲線について、ご説明したいと思います。
走行性能曲線とは、各変速ギヤにおける、速度と駆動力と走行抵抗、それに回転数を表した、盛り沢山のグラフです。
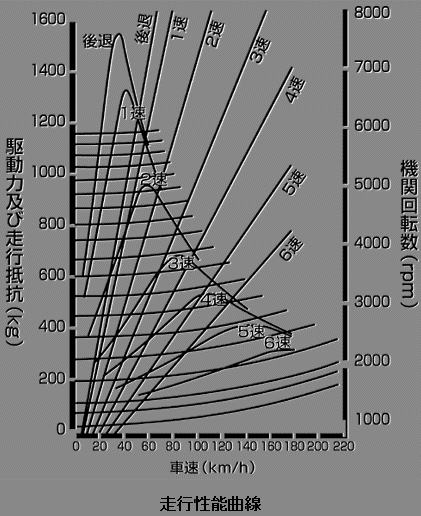
図1:5代目(BNR34型)スカイラインGT-Rの走行性能曲線
これによって、最高スピードや、最適なギヤのシフトタイミング等が分かります。
以前は自動車カタログの裏に付いていたのですが、昨今はATが主流になったためか、この走行性能曲線を表示したカタログは殆ど見当たらなくなってしまいました。
このため、本章を書き上げる意味が非常に薄れていたのですが、だったら自分で作ってみれば良いのだと思い付き、書き上げた次第です。
となると対象の車種を何にするかですが、ここではトルクカーブが特徴的なS660の走行性能曲線を作ってみたいと思います。

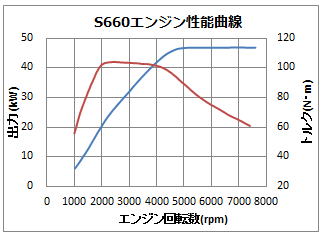
図2:ホンダS660とそのエンジン性能曲線
これが描ければ、単なる感覚的な試乗レポートを読まないでも、S660の本当の走行性能が分かります。
以下の手順で進めていけば、エクセルの使える方でしたらどなたでも作れると思いますので、是非ご自分の愛車の走行性能曲線を描いてみて頂ければと思います。
1. エンジントルク
それでは先ず、HP等に公表されているエンジン性能曲線からトルクカーブを読み取ります。
トルクカーブを読み取ると言っても、トルクカーブの画像(イメージ)を読み取るのではなく、トルクカーブからエンジンの回転数とトルク値を読み取ります。
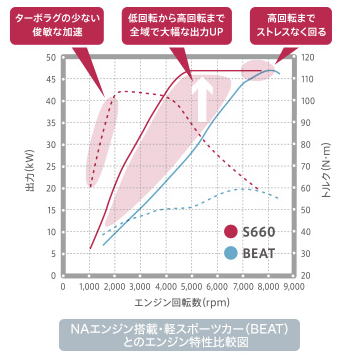
図3:ホンダS660とBEATのエンジン性能曲線
例えば上のホンダS660のトルクカーブ(赤の破線)を見ますと、1,000回転のトルクが32N・m、2,000回転のトルクが60N・mとなっています。
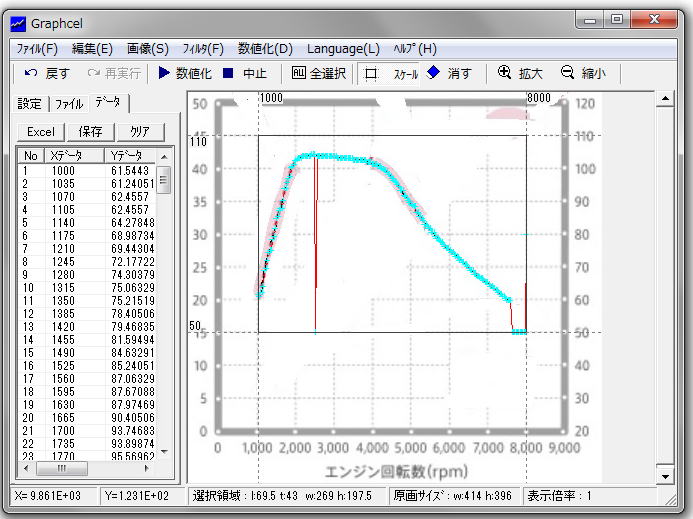
ですが、これを1000回転から8000回転まで細かく一つずつ読むのは大変なので、ここでは無料ソフトのGraphcel 1.11を使わせて頂きます。
このソフトを使って、上のトルクカーブからS660のエンジン回転数とトルク値を、カーブが滑らかに描ける程度(ここでは200ポイントを採取)に読み取ります。
そして、読み取ったデータを使って、エクセルでグラフ(ここでは散布図の平滑線を使用)を作成します。(下図参照)
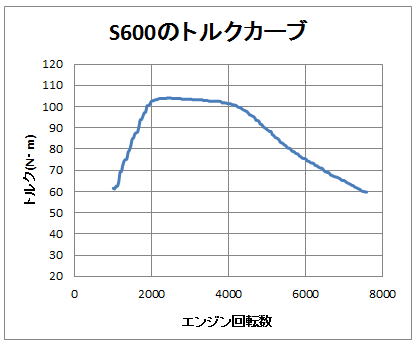
図5: グラフから数値を読み取った直後のトルクカーブ
ただし、このままですとまだ線がギザギザして美しくないので、数値を平滑処理(周囲の数値との平均処理等)してカーブを滑らかにしたのが下の図です。
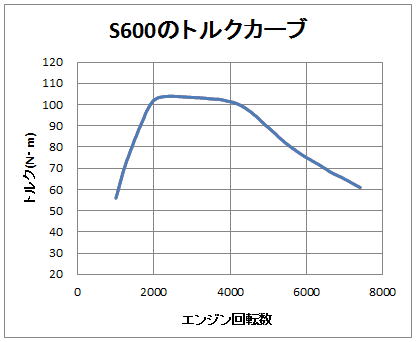
図6: 数値を平滑処理したトルクカーブ
完璧ではありませんが、much betterではないでしょうか。
2. 最終ギヤ比
エンジンのトルクカーブを入手したら、次は各変速ギヤ毎の最終ギヤ比を計算します。
でもその前に、変速比と減速比とこれから求める最終ギヤ比について、簡単に説明しておきたいと思います。
ご存じの様に、クルマはエンジンの力(トルク)によって動きます。
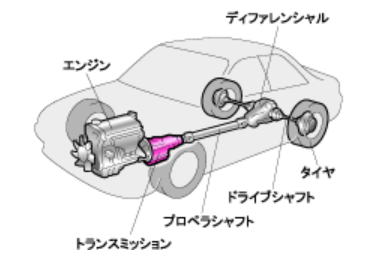
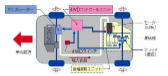
図7: クルマの駆動力伝達機構
この力は、上の図の様に、トランスミッション→ドライブシャフト→デファレンシャル→ドライブシャフトを通ってタイヤに伝わります。
この内、トランスミッシとデファレンシャルの中にはギヤが入っており、エンジンの回転速度を抑えて、駆動力を高めています。
このトランスミッションのギヤ比を変速比と呼び、デファレンシャルのギヤ比を減速比と呼びます。
そして、この二つが合わさったギヤ比を、本書では最終ギヤ比と呼ぶ事にします。
ですので、変速比と減速比を掛けたものが、最終ギヤ比になるという訳です。
最終ギヤ比=変速比x減速比
ちなみに、もし最終ギヤ比が1だとすると、エンジンが1回転するとタイヤも1回転し、タイヤの軸のトルクはエンジンの軸のトルクと同じになります。
また最終ギヤ比が2だとすると、エンジンが2回転するとタイヤが1回転する事になり、トルクは2倍になります。
以上が分かった所で、S660のスペック表(下図参照)から変速比と減速比を調べます。
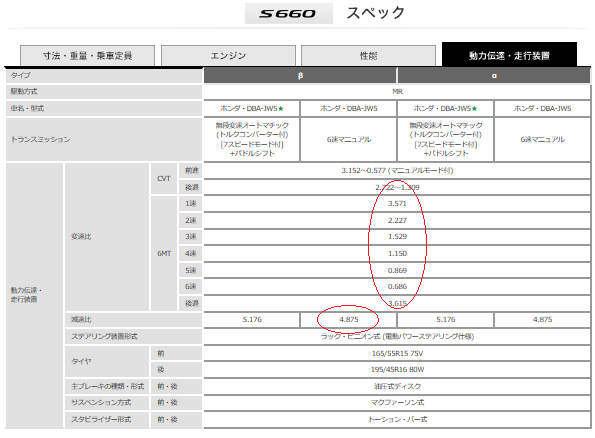
図8:S660の仕様書
それをエクセルの表に転記し、各ギヤ段毎に最終ギヤ比を求めます。
変速ギヤ別最終ギヤ比
表1: S660の変速ギヤ別最終ギヤ比
| 変速ギヤ | 1速 | 2速 | 3速 | 4速 | 5速 | 6速 |
| 変速比 | 3.571 | 2.227 | 1.529 | 1.15 | 0.869 | 0.686 |
| 減速比 | 4.875 | |||||
| 最終ギヤ比 | 17.41 | 10.86 | 7.45 | 5.61 | 4.24 | 3.34 |
もう説明は不要と思いますが、1速の最終ギヤ比である17.41は、変速比の3.751と減速比の4.857を掛けたものになります。
また1速の最終ギヤ比17.41とは、エンジンが17.41回転するとタイヤが1回転し、タイヤの軸のトルクはエンジンの軸トルクの17.41倍になる事を意味します。
3. 回転数と速度
最終ギヤ比が分かった所で、次に各変速ギヤ毎にエンジンの回転数を上げた場合の速度を求めます。
そのためには、タイヤの外径が必要ですので、S660の後輪のタイヤサイズを調べ、それからネットでタイヤの外径を調べます。
S660の場合、以下の様になります。
| 後輪タイヤ | サイズ | 外径 |
| 195/45R16 80W | 582mm |
前項でご説明しました様に、変速ギヤを1速にした場合、エンジンが17.41回転するとタイヤが1回転する事になります。
という事は、エンジンが17.41回転するとタイヤが1回転し、1827(=582x3.14)mm進む事になります。
ですので、もしエンジンが1分間に8,000回転回ったとすると、以下の様に1時間で50km進む事になります。
582mm x 3.14 ÷ 17.41 x 8000rpm x 60min/h ÷ 1000mm/m ÷ 1000m/km=50km/h
同じ様に2速から6速まで計算して表にします。
ギヤ別の回転数と速度の関係
(rpm)
表3: S660のギヤ別の回転数と速度の関係
| 速度(km) | 1速 | 2速 | 3速 | 4速 | 5速 | 6速 |
| 1 | 159 | 99 | 68 | 51 | 39 | 30 |
| 50 | 7,935 | 4,948 | 3,397 | 2,555 | 1,931 | 1,524 |
| 100 | 9,897 | 6,795 | 5,110 | 3,862 | 3,049 | |
| 150 | 7,666 | 5,793 | 4,573 | |||
| 200 | 7,723 | 6,097 |
表3: S660のギヤ別の回転数と速度の関係
さらにこれをグラフにすると、以下の様になります。
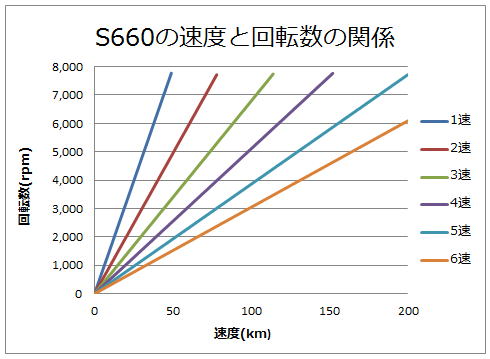
図9: S660の速度と回転数の関係
ちなみに、X軸とY軸が入れ替わっていますが、これに似たグラフがホンダのHPにも載っていしましたので、参考で載せておきます。
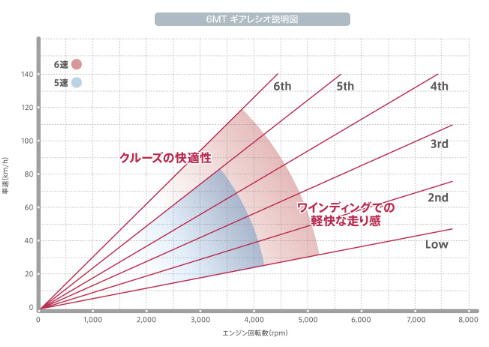
図10: S660の公式ギヤレシオ
これを見ると、6速の4,500回転で140km/hですが、こちらの計算では4500回転で148km/hです。
ピッタリではないものの、凡(おおよ)そ合っていそうです。
なおこの6%ほどの数値の違については、こちらは標準的なタイヤ外径で算出したのに対して、本田は実際のタイヤ外径もしくはヨコハマタイヤの仕様書の値を使って算出したと思われます。
ですので、S660の後輪タイヤの実外径は、582mmではなく550mmの様です。
4. 変速ギヤ毎の駆動力曲線
それでは次に、各変速ギヤ毎のタイヤの駆動力を求めます。
既に各回転数毎のトルクと各回転数毎の速度が分かっていますので、両者に共通の回転数を元にして、速度とトルクの関係を導き出します。
そしてそのトルクに、最終ギヤ比を掛けて更にタイヤの半径で割ればタイヤの駆動力が求められます。
具体的には、エクセルを使って1速から6速までの以下の様な表を作成します。
| 速度 (km/h) |
1速 | 2速 | ||||
| 回転数(rpm) | トルク(N・m) | 駆動力(N) | 回転数(rpm) | トルク(N・m) | 駆動力(N) | |
| 0 | 0 | 0 | ||||
| 1 | 159 | 99 | ||||
| 2 | 317 | 198 | ||||
| 3 | 476 | 297 | ||||
| 4 | 635 | 396 | ||||
| 5 | 793 | 495 | ||||
| 6 | 952 | 594 | ||||
| 7 | 1111 | 63 | 3753 | 693 | ||
| 8 | 1270 | 71 | 4269 | 792 | ||
| 9 | 1428 | 80 | 4783 | 891 | ||
| 10 | 1587 | 86 | 5167 | 990 | ||
| 11 | 1746 | 94 | 5607 | 1089 | 410 | 2253 |
| 12 | 1904 | 99 | 5932 | 1188 | 457 | 2514 |
| 13 | 2063 | 103 | 6142 | 1287 | 498 | 2737 |
| 14 | 2222 | 104 | 6195 | 1386 | 532 | 2924 |
| 15 | 2380 | 104 | 6216 | 1484 | 554 | 3047 |
| 16 | 2539 | 104 | 6218 | 1583 | 586 | 3222 |
| 17 | 2698 | 104 | 6205 | 1682 | 617 | 3391 |
| 18 | 2856 | 104 | 6192 | 1781 | 648 | 3562 |
| 19 | 3015 | 103 | 6185 | 1880 | 673 | 3699 |
| 20 | 3174 | 103 | 6172 | 1979 | 685 | 3768 |
| 21 | 3333 | 103 | 6164 | 2078 | 697 | 3830 |
①一番左の列に、速度を1km/hから順番に記入します。
②2番目の列に、その速度に対応した回転数を記入します。これは表3から求められます。
③3番目の列に、その回転数に対応したトルクを記入します。これは図6のトルクカーブから求められます。
④4番目の列に、そのトルクに対応した駆動力を記入します。1速の場合でしたら、トルクに最終ギヤ比の17.41を掛けて、更にタイヤの半径である0.291mで割れば求められます。
この表から作ったグラフが以下になります。
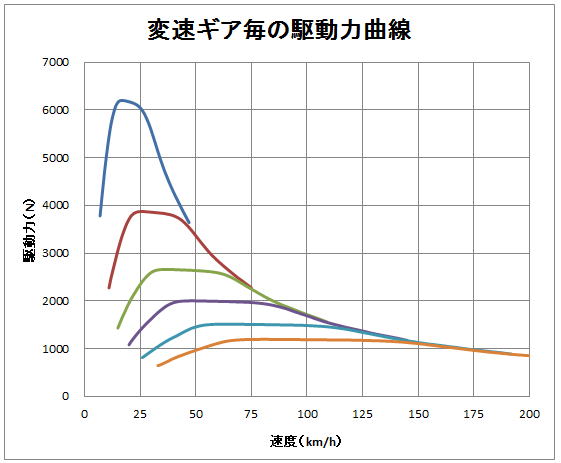
図11: S660の各変速ギヤ毎の駆動力曲線
何となく、それらしく見えませんか?
5. 走行抵抗
最後は走行抵抗です。
これは主に車重と、タイヤの摩擦係数、それに空気抵抗なのですが、簡単には調べられないので、似た車種の走行抵抗を参考にしたいと思います。
調べた所、ホンダビートの走行性能曲線がありましたので、その走行抵抗を流用したい思います。
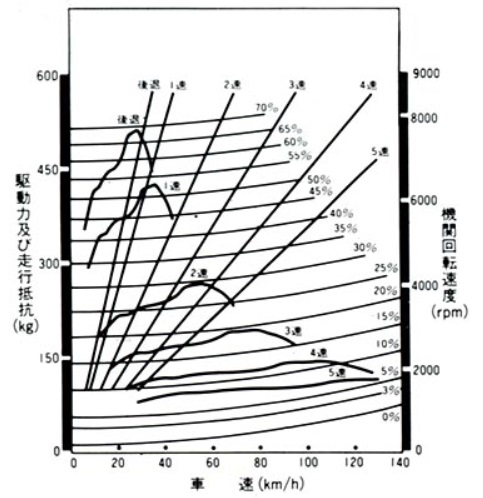
図12: ホンダビートの走行性能曲線
トルクカーブと同じ様に、Graphcel 1.11で走行抵抗のカーブを読み込みます。
S660で何度の急斜面を登れるか気にする方も居らっしゃらないと思いますので、5%まで入手しておけば十分でしょう。
これから抜き出したのが以下のグラフです。
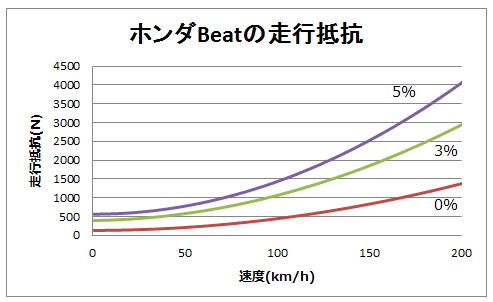
図13: ホンダビートの走行抵抗曲線
0%、3%、5%とは斜面の勾配率を表しており、角度に直すとそれぞれ0度、1.7度、2.9度になります。
ちなみに箱根の最大勾配率は13%(7.4度)です。
6. 走行性能曲線
これですべての情報が揃いましたので、全てのグラフを合体すれば走行性能曲線の完成です。
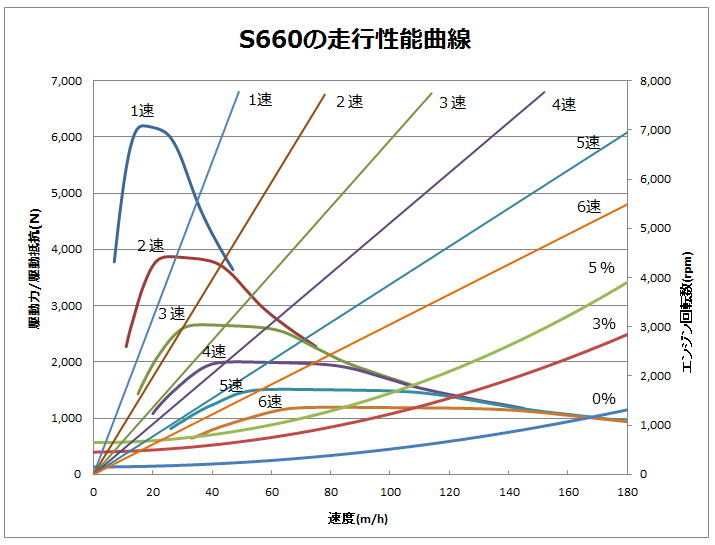
図14: S660の走行性能曲線
そして、これから分かるのは、以下の通りです。
最高速度
平地での最高速度は、勾配率0%の駆動抵抗と駆動力が交わった所になります。
この場合、170m/h辺りですが、さすがに軽自動車でそこまで出す事は不可能でしょう。
推測ですが、駆動抵抗を流用したビートの重量が760kg、S660の重量が830kgで、さらに前面投影面積もS660の方が大きいでしょうから、S660の本当の駆動抵抗はビートの 1~3%の中間のラインではないでしょうか。
だとする最高速度は 140km/h近辺となり、大凡それらしい数値になります。
シフトタイミング
走行性能曲線におけるシフトタイミングは、二つの駆動力曲線が交わった所と言えます。
この走行性能曲線を描く前は、最速で走る場合のシフトタイミングは、トルクが落ち始める前の5,000回転辺りだと思っていました。
ところがこれを見る限り、常にレッドゾーンの始まる7,600回転まで回した方が、早く走れる事が分かります。

図15: 7,600回転からレッドゾーンになるS660(MT)の回転計
例えば1速の駆動曲線を見ると、常に2速の駆動曲線より上にありますので、もし5,000回転でシフトアップしたら、途端に駆動力が低下し、加速が鈍くなります。
ただしそれから暫くトルクの山が続きますので、5,000回転でシフトチェンジした方が、感覚的には気持ちが良いかもしれません。
最高加速
走行性能曲線を見る事によって、一番加速が良いのはいつかも分かります。
それは駆動力曲線が一番急峻(きゅうしゅん)に立ち上がる所です。
ですので最高加速については、(当然ながら)1速の20kmに達するまでです。
ただしそれは余りのも短時間ですので、感覚的には多少時間的な余裕のある3速辺りではないかと思うのですが、いかがでしょうか。
走行性能曲線をご理解頂いた所で、続いてはトルクと加速度の関係についてお話したいと思います。
トルクが分かれば、ニュートンの第2法則を使ってGT-Rの加速度が求められますので、是非覗いてみて頂ければと思います。